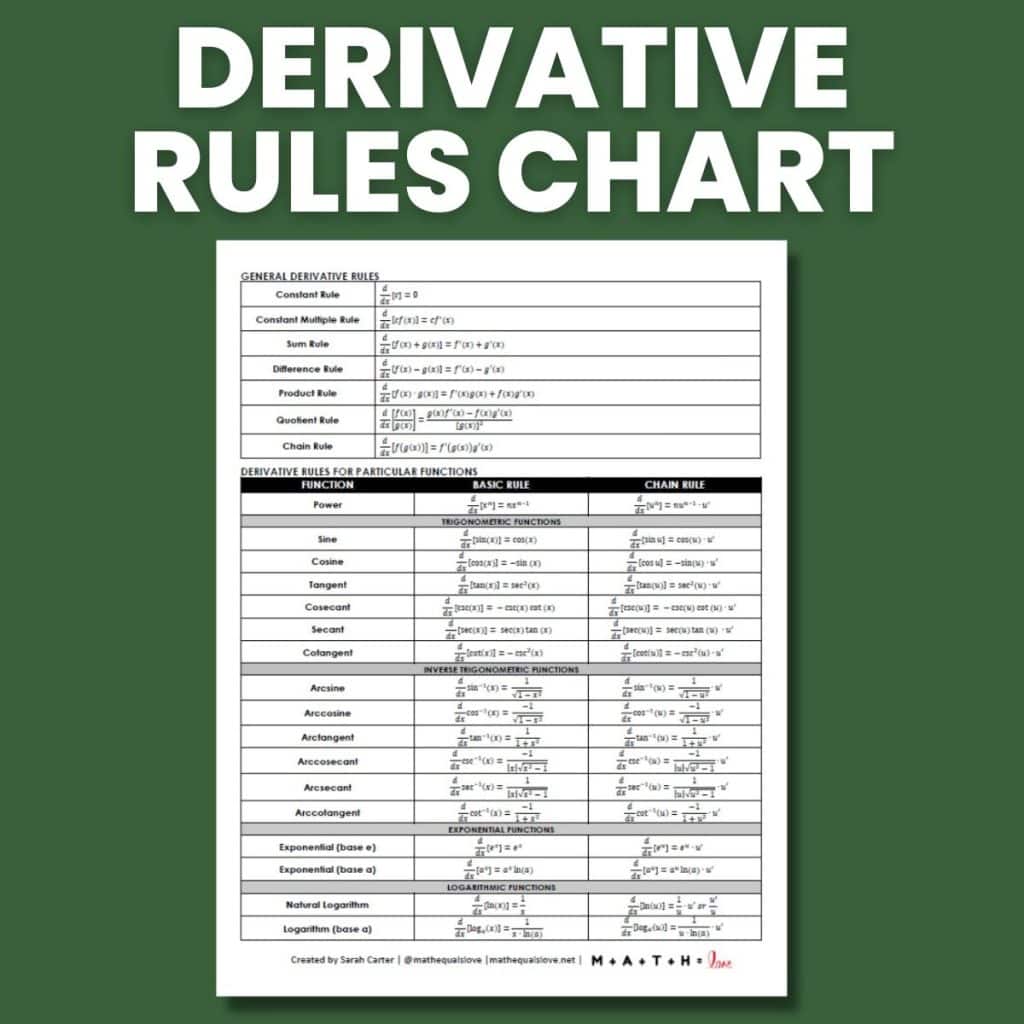
Derivative Cheat Sheet - Then there exists a number c such that a < c < b and f ( c ) = m. If y = f ( x ) then all of the following are. These rules are all generalizations of the above rules using the chain rule. Below is a list of all the derivative rules we went over in class. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Integral calculator derivative calculator algebra calculator matrix calculator more.
Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). These rules are all generalizations of the above rules using the chain rule. If y = f ( x ) then all of the following are. Integral calculator derivative calculator algebra calculator matrix calculator more. Then there exists a number c such that a < c < b and f ( c ) = m. Below is a list of all the derivative rules we went over in class.
These rules are all generalizations of the above rules using the chain rule. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If y = f ( x ) then all of the following are. Integral calculator derivative calculator algebra calculator matrix calculator more. Then there exists a number c such that a < c < b and f ( c ) = m. Below is a list of all the derivative rules we went over in class.
Derivatives and Integrals Cheat Sheet Download Printable PDF
Then there exists a number c such that a < c < b and f ( c ) = m. These rules are all generalizations of the above rules using the chain rule. Below is a list of all the derivative rules we went over in class. Suppose that f ( x ) is continuous on [a, b] and let.
Calculus Cheat Sheet Derivatives Reduced PDF PDF Maxima And Minima
These rules are all generalizations of the above rules using the chain rule. Below is a list of all the derivative rules we went over in class. If y = f ( x ) then all of the following are. Integral calculator derivative calculator algebra calculator matrix calculator more. Then there exists a number c such that a < c.
Derivatives Cheat Sheet PDF
These rules are all generalizations of the above rules using the chain rule. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If y = f ( x ) then all of the following are. Integral calculator derivative calculator algebra calculator matrix.
Integral Rules Cheat Sheet vrogue.co
Integral calculator derivative calculator algebra calculator matrix calculator more. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Then there exists a number c such that a < c < b and f ( c ) = m. If y = f.
Derivative Rules Cheat Sheet Calculus Ace Tutors Blog
Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If y = f ( x ) then all of the following are. These rules are all generalizations of the above rules using the chain rule. Then there exists a number c such.
Calculus Integrals Reference Sheet (with Formulas) EEWeb
Then there exists a number c such that a < c < b and f ( c ) = m. Integral calculator derivative calculator algebra calculator matrix calculator more. Below is a list of all the derivative rules we went over in class. If y = f ( x ) then all of the following are. These rules are all.
Derivative Rules Cheat Sheet
Integral calculator derivative calculator algebra calculator matrix calculator more. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Then there exists a number c such that a < c < b and f ( c ) = m. Below is a list.
Math Cheat Sheet Derivative ShortCut Formulas Download Printable PDF
If y = f ( x ) then all of the following are. These rules are all generalizations of the above rules using the chain rule. Then there exists a number c such that a < c < b and f ( c ) = m. Integral calculator derivative calculator algebra calculator matrix calculator more. Below is a list of.
Derivatives Cheat Sheet 5/2/24, 807 PM Derivatives Cheat Sheet
Integral calculator derivative calculator algebra calculator matrix calculator more. If y = f ( x ) then all of the following are. Then there exists a number c such that a < c < b and f ( c ) = m. Below is a list of all the derivative rules we went over in class. These rules are all.
The Essential Derivative Cheat Sheet Your Quick Guide to Calculus
If y = f ( x ) then all of the following are. Below is a list of all the derivative rules we went over in class. Then there exists a number c such that a < c < b and f ( c ) = m. Integral calculator derivative calculator algebra calculator matrix calculator more. Suppose that f (.
Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More.
If y = f ( x ) then all of the following are. Below is a list of all the derivative rules we went over in class. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). These rules are all generalizations of the above rules using the chain rule.