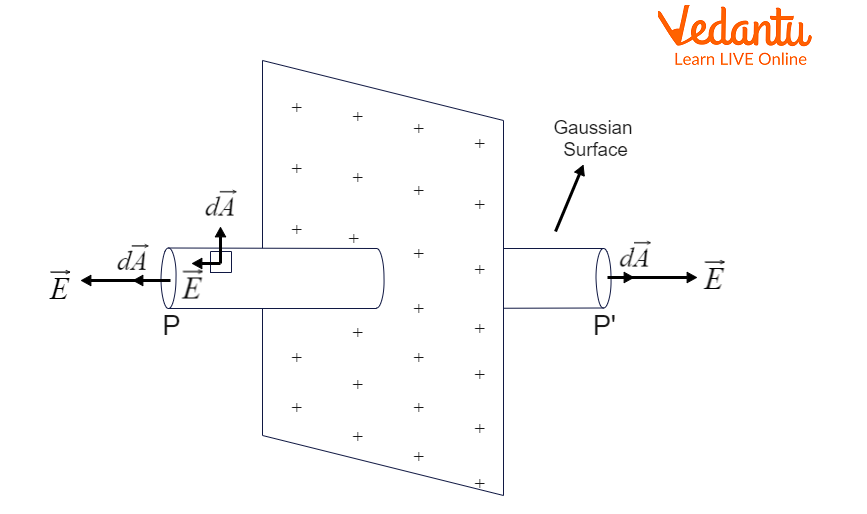
Electric Field For Infinite Sheet - This is independent of the. Therefore only the ends of a cylindrical gaussian surface. Using gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the. For an infinite sheet of charge, the electric field will be perpendicular to the surface. (1.6.12) (1.6.12) e = σ 2 ϵ 0. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain.
This is independent of the. All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain. Therefore only the ends of a cylindrical gaussian surface. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. (1.6.12) (1.6.12) e = σ 2 ϵ 0. Using gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the. For an infinite sheet of charge, the electric field will be perpendicular to the surface.
For an infinite sheet of charge, the electric field will be perpendicular to the surface. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain. (1.6.12) (1.6.12) e = σ 2 ϵ 0. This is independent of the. Using gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the. Therefore only the ends of a cylindrical gaussian surface.
Electric field due to infinite non conducting sheet of surface charge
This is independent of the. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. (1.6.12) (1.6.12) e = σ 2 ϵ 0. For an infinite sheet of charge, the electric field will be perpendicular to the surface. Using gauss’s law, prove that the electric field at.
electrostatics Electric field due to uniformly charged infinite plane
This is independent of the. For an infinite sheet of charge, the electric field will be perpendicular to the surface. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. Using gauss’s law, prove that the electric field at a point due to a uniformly charged infinite.
Electric Field due to Infinite Plane Important Concepts for JEE
For an infinite sheet of charge, the electric field will be perpendicular to the surface. (1.6.12) (1.6.12) e = σ 2 ϵ 0. Therefore only the ends of a cylindrical gaussian surface. This is independent of the. All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain.
electrostatics Electric field due to uniformly charged infinite plane
All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. For an infinite sheet of charge, the electric field will be perpendicular to the surface. Using.
Electric field intensity due to a thin infinite plane sheet of charge
For an infinite sheet of charge, the electric field will be perpendicular to the surface. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. Therefore only the ends of a cylindrical gaussian surface. (1.6.12) (1.6.12) e = σ 2 ϵ 0. This is independent of the.
homework and exercises Find the electric field of an infinite sheet
Therefore only the ends of a cylindrical gaussian surface. All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain. This is independent of the. For an infinite sheet of charge, the electric field will be perpendicular to the surface. Use gauss’s law to find the electric field caused by.
Solved The electric field on either side of an infinite
All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain. Therefore only the ends of a cylindrical gaussian surface. For an infinite sheet of charge, the electric field will be perpendicular to the surface. This is independent of the. Using gauss’s law, prove that the electric field at a.
SOLUTION 3 electric field infinite sheet Studypool
Therefore only the ends of a cylindrical gaussian surface. This is independent of the. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. (1.6.12) (1.6.12) e = σ 2 ϵ 0. Using gauss’s law, prove that the electric field at a point due to a uniformly.
SOLUTION 3 electric field infinite sheet Studypool
Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. Using gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the. Therefore only the ends of a cylindrical gaussian surface. (1.6.12) (1.6.12) e = σ.
homework and exercises Electric field of an infinite sheet of charge
Using gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the. This is independent of the. (1.6.12) (1.6.12) e = σ 2 ϵ 0. For an infinite sheet of charge, the electric field will be perpendicular to the surface. Use gauss’s law to find the electric field caused.
This Is Independent Of The.
For an infinite sheet of charge, the electric field will be perpendicular to the surface. Use gauss’s law to find the electric field caused by a thin, flat, infinite sheet with a uniform positive surface charge density $\sigma$. All we have to do is to put α = π/2 α = π / 2 in equation 1.6.10 to obtain. Therefore only the ends of a cylindrical gaussian surface.
Using Gauss’s Law, Prove That The Electric Field At A Point Due To A Uniformly Charged Infinite Plane Sheet Is Independent Of The.
(1.6.12) (1.6.12) e = σ 2 ϵ 0.